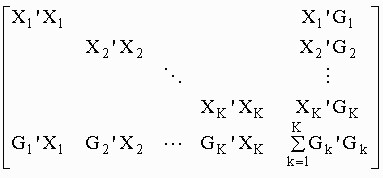Lange's Covariance Matrix (LCM):


which is the inverse of:


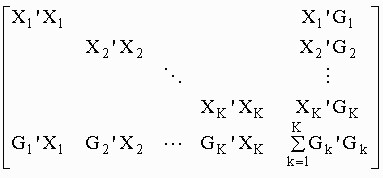
and that renders the exact precision of Wolf's analytic solution:


to Helmert's problem:

which canonical form can always be achieved, for example, through performing a generalized Canonical Correlation Analysis (gCCA) on the observation errors. It would though be advantageous to find a most meaningful way of clustering the data into mutually uncorrelated blocks which would then make the best sense also physically.

This semi-analytic inversion is known in Geodesy as the Helmert-Wolf blocking (HWB) method and it is central to Satellite Geodesy. The LCM formula above is seminal to the Fast K- Filtering (FKF) method which, in turn, is a "must" to all mobile positioning, navigation, forecasting and control appliances as well as to Numerical Weather Prediction (NWP) systems that comply with the highest precision, integrity and safety rules and standards.