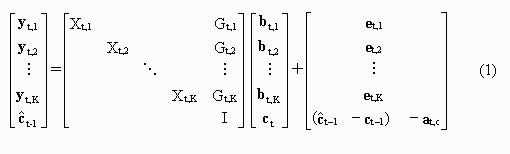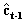Any linearized joint regression equation system of different observation series can be written out in the Canonical Block-Angular (CBA) form as follows:

where vectors y_t,1, y_t,2,…, y_t,K and e_t,1, e_t,2,…, e_t,K represent the measurements and their errors, respectively, from the different observation series (k = 1, 2,..., K) during an observing period t (t = 1, 2,...). Vectors b_t,1, b_t,2,…, b_t,K represent entirely unknown regression parameters. Those regression parameters that are common to several observation series are represented here by a common vector c_t whose prior estimates at time t-1 are given by . Matrices X_t,1, X_t,2,…, X_t,K and G_t,1, G_t,2,…, G_t,K are the Jacobians that are related to the unknown parameters and to the common parameters, respectively. Vector a_t,c represents random errors of the common parameters that typically stem from various calibration drifts and/or modeling errors.
Moreover, it is possible to determine an additional set of common parameters for transforming the joint covariance matrix of the residuals e_t,1, e_t,2,…, e_t,K into a strictly block-diagonal form. This can be done by making use of those CANONICAL COMMON FACTORS (e.g. Empirical Orthogonal Functions G_t,1, G_t,2,…, G_t,K) that are found by performing a Principal Component Analysis on all the residuals after they have first been orthonormalized separately within every block k (k = 1, 2,..., K). This computational procedure for finding the conventional Canonical Correlations between only two blocks (K = 2) of data was described by Lange already in 1969. These tedious preparatory measures are required for speeding up the optimal FKF computations in realtime. Reference is also made to the discussion on Multivariate Statistical Methods in Statistical Calibration of Observing Systems (Lange, 1999), see page 16, and PCT/FI96/00621 (Lange, 1997), see pages 11-12.